Last week, we wrapped up our winter sessions with over 50 elementary school math teams. Part of these sessions are devoted to having teachers work together to solve problems. Having teachers “do the math” helps brings meaning to important topics in mathematics education. We gave the following problem, from Van de Walle:
In a particular small town, 2/3 of the men are married to 3/5 of the women. What fraction of the entire population are married?
This is a challenging problem, but only because traditional algorithms get in the way of sense-making methods. The gut reaction is to do something with common denominators. Time after time, with each group, primary and intermediate. Through questioning, the mistake can be recognized.
“In this context, what does the 15 over here represent?” [points to 10/15]
“The total number of men.”
“And over here?” [points to 9/15]
“The total number of wom–OOOOOh…”
Sometimes, it takes longer to reach an ‘OOOOOh’:
“What does the 10 represent?”
“The number of married men.”
“And the 9?”
“The number of married wom–OOOOOh…”
Once teachers realize that having 10 men married to 9 women is somewhat problematic, most model the problem using colour tiles. Two out of three men being married becomes four out of six and six out of nine. Three out of five women being married is equivalent to six out of ten. Six pairs of husbands and wives can be formed. We have 12 out of 19 people being married.
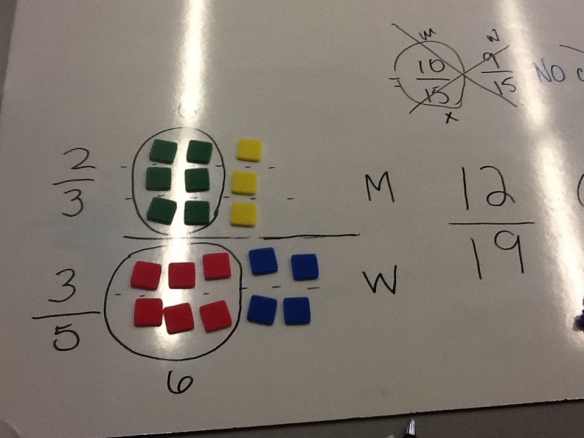Others think logically to solve the problem. The number of husbands must equal the number of wives. The number of husbands and wives are represented by the numerators. Therefore, the numerators must be made equal. With all due respect to Dr. Math, it just makes sense.
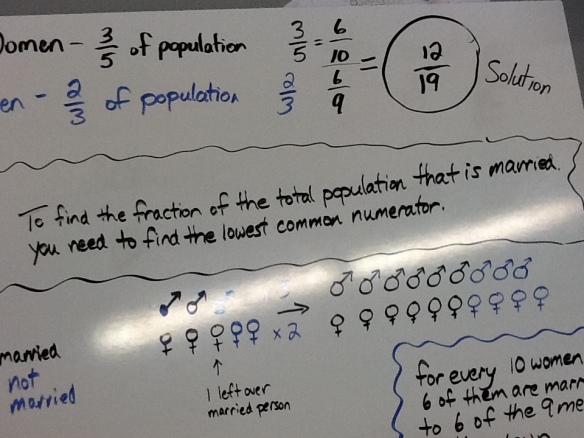The use of manipulatives to construct meaning continues to be a focus of teachers involved in the numeracy project, both for themselves and for their students. Long before I became involved in this project, my fellow Numeracy Helping Teachers (Marc Garneau, Selina Millar, Sandra Ball, and Shelagh Lim) worked tirelessly to set a climate in which teachers and students felt comfortable using a variety of manipulatives.
At these sessions, we present teachers with problems, not practice. It’s a pleasure to work with such an amazing group of educators so willing to explore, take risks, and persevere. But as much fun as these sessions with teachers have been, I’m looking forward to the real fun: problem-solving with their students.
Update (2020/01/18)
A much more inclusive context!
Chris Hunter 
Very cool, Chris. I’m going to totally use this problem with my colleagues, if we get another problem solving session together.
The logical way to solve this that jumped out at me was to do it algebraically. Let X be the number of men, and let Y be the number of women in the town. The total number of people in the town is X+Y. First start off assuming that the number of men and women in the town that are married must be equal (which i believe is one of your assumptions, so we have to rule out same-sex marriage or polygamy). So we have Eq 1):
2/3X = 3/5Y.
Now What do we want to solve? The number of people married over the total number of people, or Eq 2):
{(2/3)X+(3/5)Y} / {X+ Y}.
Substituting Eq 1 in Eq2 and doing the arithmetic, I get 12/19.
BTW, I just clicked on Dr. Math’s answer, I didn’t realize it was the same way as mine before I posted haha. I was uncomfortable with your idea of “adding the numerators” is because we’re not adding 2/3 and 3/5, we’re adding 2/3 of *something* and 3/5 of *something else*. By adding the numerators, you’re making an assumption that the lowest common numerator will give you the correct *something* and *something else* as denominators. Does it scale if the number of people married is not the lowest common numerator? Say 6? or 30? or 3000? After doing some algebra, I convinced myself it does, but until then, it was handwaving.
Sorry, I should have been more careful when I wrote that post. Everywhere where I wrote “adding the numerators”, I meant “finding the lowest common numerator and adding the denominators.”
@James One group (of K-3 teachers) started with your Equation 1: (2/3)x = (3/5)y. They divided both sides by 2/3 which gave them x = (9/10)y. Next, they divided both sides by y which gave them x/y = 9/10. That is, the ratio of men (total) to women (total) is 9 to 10. Two-thirds of 9 and three-fifths of 10 gave them 6 men married to 6 women. We can use 18 and 20 or 90 and 100. It’s the ratio that matters.
I used an algebraic approach when I was first given this problem but I didn’t find it as convincing. Above, I wasn’t concerned with finding correct denominators. The correct denominators (the whole) are a natural consequence of finding the correct numerators (the part). 6, 12, 300… it doesn’t matter, so long as the number of men married to women (the part in the first fracton) matches the number of women married to men (the part in the second fraction). How could it be otherwise? (In the photo above, one group wrote “you need to find the lowest common numerator.” In fact, any common numerator will do.)
We did discuss the assumptions re: marriage. Polygamy would either make the problem unsolvable or much more open (Ha!). It’s a decades-old problem: a new context is needed. Some teachers suggested mixed tennis/dancing partners. This could work.